2000 Rpm In Rad S
deazzle
Sep 16, 2025 · 6 min read
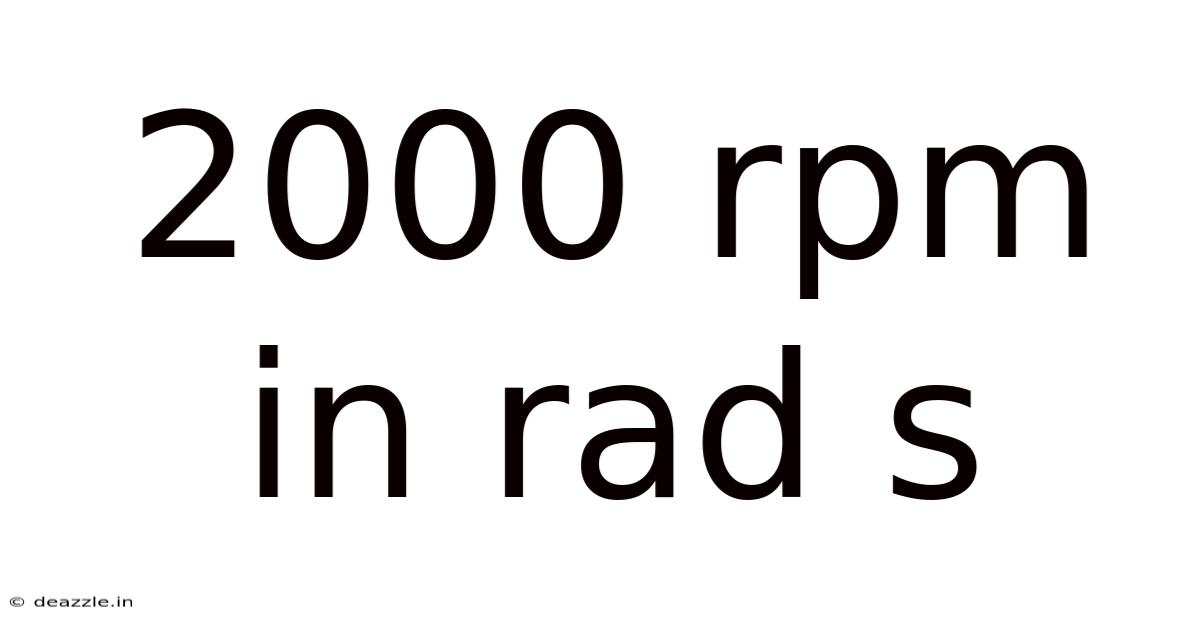
Table of Contents
Understanding 2000 RPM in rad/s: A Comprehensive Guide
Converting units of rotational speed is a fundamental concept in physics and engineering. Frequently, we encounter rotational speeds expressed in revolutions per minute (RPM), a practical unit for everyday applications. However, for many calculations, especially in physics and engineering, the standard unit of angular velocity is radians per second (rad/s). This article provides a comprehensive understanding of how to convert 2000 RPM to rad/s and explores the underlying concepts involved, including the relationship between linear and angular velocity. We will also delve into practical applications and address frequently asked questions.
Introduction: RPM vs. rad/s
Revolutions per minute (RPM) represents the number of complete rotations an object makes around a central axis in one minute. It's a widely used unit in everyday contexts, such as describing the speed of a motor, engine, or turntable. Radians per second (rad/s), on the other hand, is the standard unit of angular velocity in the International System of Units (SI). It represents the rate of change of an angle (in radians) with respect to time (in seconds). Understanding the difference and how to convert between these units is crucial for various applications.
The Conversion Process: 2000 RPM to rad/s
The conversion from RPM to rad/s relies on two key relationships:
-
Revolutions to Radians: One complete revolution is equal to 2π radians. This is because a circle encompasses 2π radians.
-
Minutes to Seconds: One minute is equal to 60 seconds.
Therefore, to convert 2000 RPM to rad/s, we follow these steps:
-
Convert revolutions to radians: 2000 revolutions * 2π radians/revolution = 4000π radians
-
Convert minutes to seconds: The speed is currently expressed as 4000π radians/minute. To convert to rad/s, we divide by 60 seconds/minute: (4000π radians/minute) / (60 seconds/minute) = (4000π/60) rad/s
-
Simplify: (4000π/60) rad/s simplifies to (200π/3) rad/s. This is the exact value.
-
Approximate value: Using the approximation π ≈ 3.14159, we get an approximate value of (200 * 3.14159 / 3) rad/s ≈ 209.44 rad/s
Therefore, 2000 RPM is approximately equal to 209.44 rad/s.
Deeper Dive: Understanding Angular Velocity
Angular velocity (ω) describes how fast an object rotates or revolves around a central axis. It's a vector quantity, meaning it has both magnitude and direction. The magnitude represents the rate of rotation, while the direction is along the axis of rotation (determined by the right-hand rule).
The relationship between angular velocity (ω) and linear velocity (v) is given by:
v = ωr
where:
- v is the linear velocity (m/s)
- ω is the angular velocity (rad/s)
- r is the radius of the circular path (m)
This equation is fundamental in understanding the connection between rotational motion and linear motion. If you know the angular velocity and the radius, you can easily calculate the linear velocity of a point on the rotating object. Conversely, if you know the linear velocity and radius, you can find the angular velocity.
Practical Applications of Angular Velocity Conversions
The conversion between RPM and rad/s is essential in numerous applications across various fields:
-
Mechanical Engineering: Designing and analyzing rotating machinery like motors, turbines, and gears requires accurate conversion between RPM and rad/s for calculating torque, power, and stress.
-
Robotics: In robotics, precise control of motors and actuators necessitates the use of rad/s for programming and controlling robot movements.
-
Aerospace Engineering: Calculating the rotational speed of aircraft propellers or helicopter rotors involves conversion between RPM and rad/s for performance analysis and stability calculations.
-
Automotive Engineering: Analyzing engine speed, wheel rotation, and transmission ratios often requires working with both RPM and rad/s for performance analysis and design optimization.
-
Physics: Many physics problems involving rotational motion, such as calculating centripetal acceleration and angular momentum, require the use of rad/s for accurate calculations.
Explanation of Radians
Radians are a fundamental unit for measuring angles in mathematics and physics. Unlike degrees, which are arbitrary units, radians are defined based on the ratio of the arc length to the radius of a circle.
One radian is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. Since the circumference of a circle is 2πr (where r is the radius), there are 2π radians in a complete circle (360 degrees). This fundamental relationship is crucial for understanding the conversion between revolutions and radians.
Frequently Asked Questions (FAQ)
Q1: Why is rad/s preferred over RPM in scientific calculations?
A1: Rad/s is the SI unit for angular velocity, making it consistent with other SI units used in physics and engineering calculations. Using rad/s simplifies formulas and avoids the need for extra conversion factors.
Q2: Can I use this conversion for any RPM value?
A2: Yes, the conversion process remains the same regardless of the RPM value. Simply substitute the given RPM value into the formula: ω (rad/s) = (RPM * 2π) / 60
Q3: What if I need to convert from rad/s back to RPM?
A3: To convert from rad/s back to RPM, use the following formula: RPM = (ω * 60) / (2π)
Q4: How does the radius of the rotating object affect the linear velocity?
A4: The radius directly affects the linear velocity. A larger radius at the same angular velocity will result in a higher linear velocity, because points farther from the axis of rotation travel a greater distance in the same amount of time. This is evident in the formula: v = ωr
Q5: Are there other units for angular velocity?
A5: Yes, although rad/s is the standard SI unit, other units exist, such as degrees per second (°/s) or revolutions per second (rev/s). However, rad/s is generally preferred in scientific and engineering contexts due to its mathematical simplicity and consistency with other SI units.
Conclusion
Converting 2000 RPM to rad/s, approximately 209.44 rad/s, is a straightforward process that involves understanding the relationship between revolutions, radians, and time. This conversion is fundamental in various fields, ranging from mechanical engineering to robotics and physics. Understanding the concept of angular velocity and its connection to linear velocity is crucial for solving problems related to rotational motion. Mastering this conversion enhances your ability to analyze and design systems involving rotating components, furthering your understanding of fundamental physics and engineering principles. Remember that the use of radians is not just a matter of unit conversion; it's fundamental to the mathematical description of rotational motion, providing a cleaner and more consistent framework for calculations.
Latest Posts
Latest Posts
-
30 Days From Nov 16
Sep 16, 2025
-
90 Days After June 15
Sep 16, 2025
-
90 Days From September 29
Sep 16, 2025
-
How Long Is 1 5 Meters
Sep 16, 2025
-
Cubic Inches To Fluid Ounces
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2000 Rpm In Rad S . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.