Rad Per Sec To Rpm
deazzle
Sep 18, 2025 · 5 min read
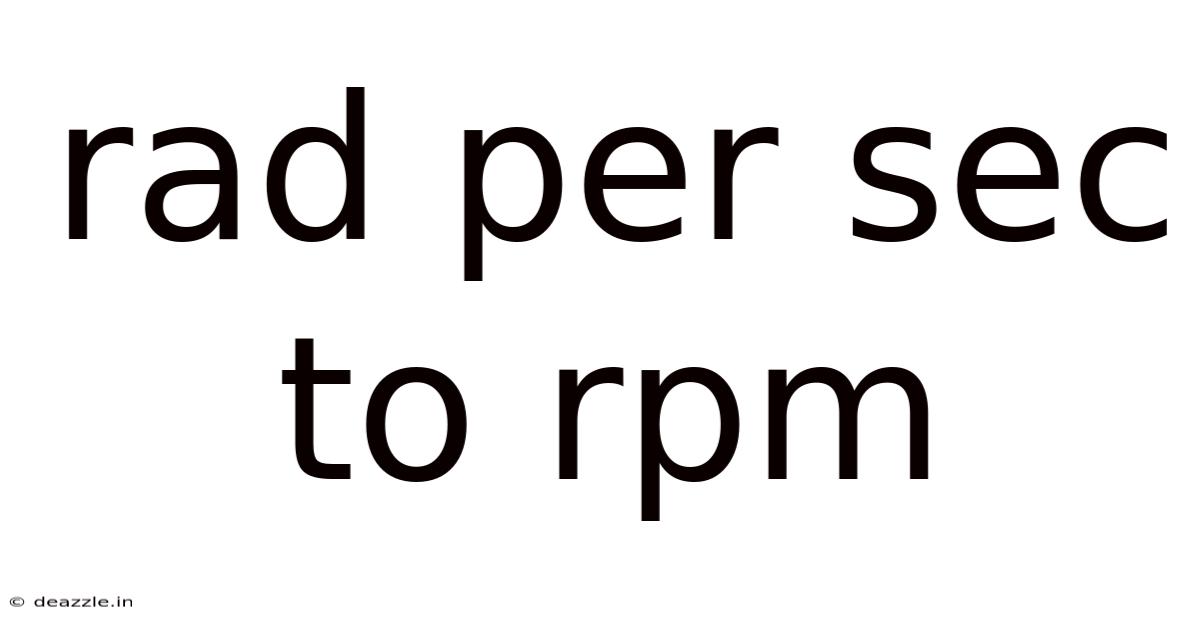
Table of Contents
Decoding the Spin: A Comprehensive Guide to Converting Rad/s to RPM
Understanding rotational speed is crucial in various fields, from engineering and physics to everyday applications like understanding the speed of a motor or a spinning disc. Often, we encounter rotational speed expressed in two common units: radians per second (rad/s) and revolutions per minute (RPM). This comprehensive guide will delve into the intricacies of converting between these units, explaining the underlying concepts and providing practical examples to solidify your understanding. We will explore the mathematical relationship, tackle common misconceptions, and answer frequently asked questions to ensure you become proficient in this essential conversion.
Understanding the Units: Rad/s and RPM
Before diving into the conversion, let's clarify the meaning of each unit:
-
Radians per second (rad/s): This unit measures angular velocity using radians. A radian is a unit of angular measurement defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle. One complete revolution around a circle encompasses 2π radians. Therefore, rad/s measures how many radians an object rotates through per second.
-
Revolutions per minute (RPM): This unit is more intuitive, simply measuring the number of complete rotations or revolutions an object makes per minute. It's commonly used to describe the rotational speed of engines, motors, and other rotating machinery.
The Mathematical Conversion: Rad/s to RPM
The core of the conversion lies in understanding the relationship between radians and revolutions, and seconds and minutes. Here's the breakdown:
-
Radians to Revolutions: As mentioned earlier, one complete revolution equals 2π radians. Therefore, to convert radians to revolutions, we divide the number of radians by 2π.
-
Seconds to Minutes: There are 60 seconds in one minute. To convert seconds to minutes, we divide the number of seconds by 60.
Combining these two steps, the complete conversion formula from rad/s to RPM is:
RPM = (rad/s) × (60 seconds/minute) × (1 revolution/2π radians)
This simplifies to:
RPM ≈ (rad/s) × 9.5493
This means you can approximately convert rad/s to RPM by multiplying the value in rad/s by 9.5493.
Practical Examples: Illustrating the Conversion
Let's solidify our understanding with some practical examples:
Example 1: A motor spins at 10 rad/s. What is its speed in RPM?
Using the formula:
RPM ≈ 10 rad/s × 9.5493 ≈ 95.49 RPM
Therefore, the motor spins at approximately 95.49 RPM.
Example 2: A spinning disc rotates at 500 RPM. What is its angular velocity in rad/s?
To convert RPM back to rad/s, we simply reverse the formula:
rad/s ≈ RPM / 9.5493
rad/s ≈ 500 RPM / 9.5493 ≈ 52.36 rad/s
Therefore, the spinning disc has an angular velocity of approximately 52.36 rad/s.
Example 3: A more complex scenario
Imagine a gear system where a smaller gear with a radius of 5 cm rotates at 15 rad/s. This smaller gear is connected to a larger gear with a radius of 10 cm. We want to find the RPM of the larger gear.
First, we find the RPM of the smaller gear:
RPM_small ≈ 15 rad/s * 9.5493 ≈ 143.24 RPM
Now, we use the gear ratio principle. The gear ratio is the ratio of the radii of the two gears (larger gear radius / smaller gear radius = 10cm / 5cm = 2). The smaller gear rotates twice as fast as the larger gear.
RPM_large = RPM_small / gear ratio = 143.24 RPM / 2 ≈ 71.62 RPM
Therefore, the larger gear rotates at approximately 71.62 RPM.
This example highlights how understanding the rad/s to RPM conversion can be a building block for solving more complex rotational mechanics problems.
Beyond the Basic Conversion: Understanding Angular Acceleration
While this article focuses primarily on converting between rad/s and RPM, it's important to briefly touch upon the concept of angular acceleration. Angular acceleration measures the rate of change of angular velocity. It's expressed in units of rad/s² (radians per second squared). Understanding angular acceleration is crucial in analyzing the dynamics of rotating systems. For example, when a motor accelerates from rest, it experiences a positive angular acceleration.
Addressing Common Misconceptions
A common misunderstanding is treating the conversion factor as a fixed, precise value. While 9.5493 is a good approximation, it's derived from the approximation of π. For extremely precise calculations, it's crucial to use the full formula and the most accurate value of π available.
Frequently Asked Questions (FAQ)
-
Q: Why are both rad/s and RPM used? A: Different fields prefer different units. Rad/s is commonly used in physics and engineering calculations because it's directly related to other angular quantities, while RPM is more intuitive and practical for everyday applications.
-
Q: Can I use this conversion for any rotating object? A: Yes, as long as the rotation is relatively uniform. For highly irregular rotations, the average angular velocity might be more meaningful.
-
Q: What about negative values? A: A negative value in rad/s simply indicates a change in the direction of rotation. The conversion formula still applies. The RPM value will also be negative reflecting the reversed direction.
-
Q: Are there online calculators for this conversion? While readily available, it is crucial to understand the underlying principles and not solely rely on calculators.
Conclusion: Mastering Rad/s to RPM Conversions
Mastering the conversion between rad/s and RPM is a valuable skill across various disciplines. This guide provided not only the formula but also the conceptual understanding, practical examples, and common pitfalls to ensure you confidently navigate this important conversion. Remember to always consider the context of the problem and choose the most appropriate unit for your application. With a clear understanding of the relationship between radians, revolutions, seconds, and minutes, you can now effectively translate rotational speeds between these units, solving a wide range of problems with precision and accuracy. This skill will undoubtedly enhance your understanding of rotational mechanics and its diverse applications.
Latest Posts
Latest Posts
-
60 Days From January 24
Sep 18, 2025
-
30 Days From October 18th
Sep 18, 2025
-
90 Days From Dec 12 2024
Sep 18, 2025
-
30 Days From October 14th
Sep 18, 2025
-
Days Since 9 17 24
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Rad Per Sec To Rpm . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.